引言
我們前幾天已經把 General Skills 完成了，所以今天開始 (已經沒剩幾天了
就至少會把六大領域各做一題以上，不過這個密碼學領域應該只會出現一天，也就是今天，
因為今天會做兩題 (有一題較簡單) ，那就開始吧～

Cryptography / Mod 26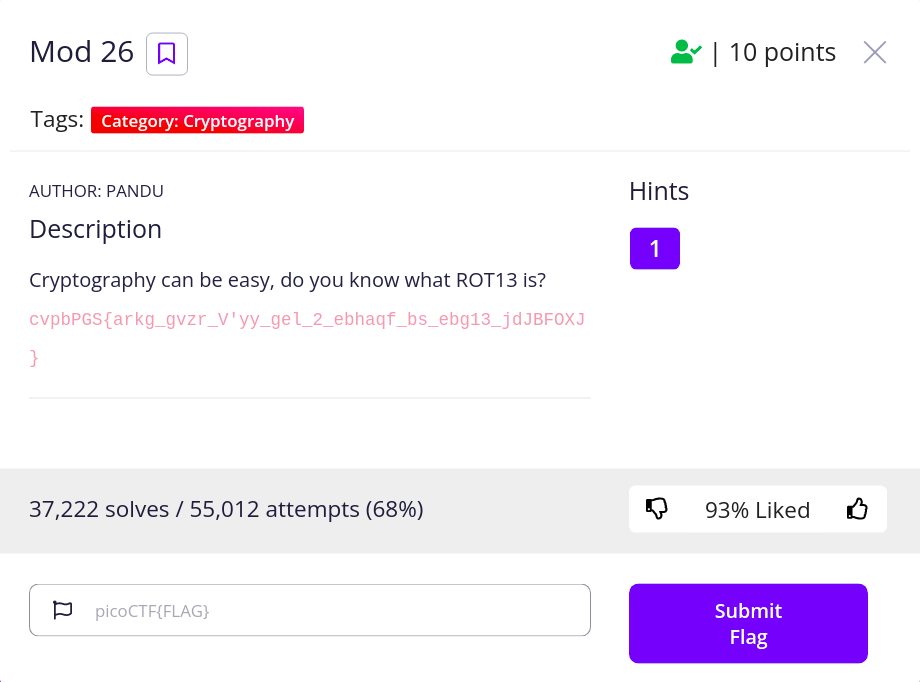

題目給了一段亂碼，但是很明顯可以看出這是 flag 格式，底線、大括號都沒有變，
然後說要用 ROT13 解決，關於 ROT13 可以看看這裡 (維基百科)，
其實簡單來講它就只是把每個字母往前往後推算幾個字母，超過 z 則回到 a 的概念，
可以算是密碼學中最簡單的方法之一了，因為一共 26 個字母，
ROT13 的移動量剛好一半，所以你對一個字母做兩次 ROT13 會回到本身。

這題有兩種解法，其一是用線上翻譯器破解，另一個是自己寫程式。
我兩個都提供給大家：

1. rot13.com 線上 ROT13 加密/解密器
   你丟明文會跑出密文，丟密文會跑出明文，它們是互相對稱的。
2. 寫個 Python 程式
   其實就是從原理下手去寫，程式貼在下方：

   s = input()
   for c in s:
       oc = ord(c)
       if oc >= ord('A') and oc <= ord('Z'):  # 大寫
           coc = chr((((oc-ord('A'))+13)%26)+ord('A'))
           print(coc, end='')
       elif oc >= ord('a') and oc <= ord('z'):  # 小寫
           coc = chr((((oc-ord('a'))+13)%26)+ord('a'))
           print(coc, end='')
       else:
           print(c, end='')
   print()
   

   只有英文大小寫需要轉換，其他符號記得要忽略。

Cryptography / Mind your Ps and Qs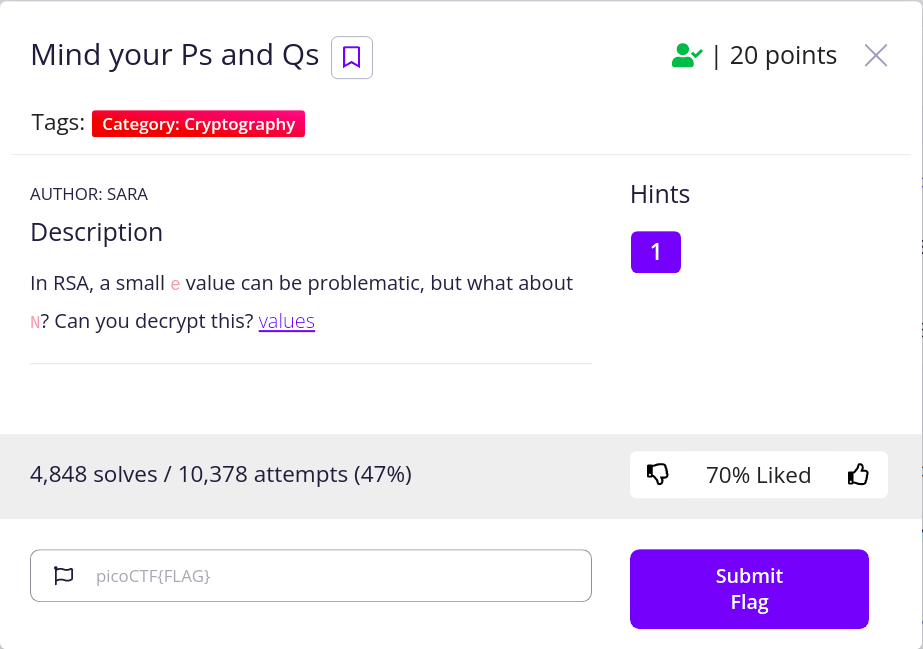

這題稍微難一點點，是考 RSA 加密，這是一種非對稱加密，
簡單來說就是加密與解密需要的鑰匙不是同一把，
加密用的叫公鑰 (e) ，會公開，解密用的叫私鑰 (d) ，不會公開，
細節可以看看維基百科的說明，這邊簡單講一下如何取得兩把鑰匙：

<從維基百科 RSA 擷取>

1. 隨意選擇兩個大的質數 p 和 q ， p 不等於 q ，計算 N=pq 。
2. 根據歐拉函數，求得
3. 選擇一個小於 r 的整數 e ，使 e 與 r 互質。並求得 e 關於 r 的乘法反元素，命名為 d（求 d 令 ）。（乘法反元素存在，若且唯若 e 與 r 互質）
4. 將 p 和 q 的記錄銷毀。

好，說簡單講其實也不簡單對吧，你只要先知道有 N, p, q, r, e, d 這些數就夠了，
其中 N, r 是由 p, q 產生，而 e 根據 r 產生， d 是 e, r 產生的。
所以其實 p, q 才是大家的父母，也就是說想破解的人找到 p, q 是至關重要的。

下面講一下如何加密與解密：
首先，明文以 n 表示，密文以 c 表示。

1. 將 n 加密成 c ：
   
   「n 的 e 次方」 除以 「N」 的餘數是 「c」
2. 將 c 解密回 n ：
   
   「c 的 d 次方」 除以 「N」 的餘數是 「n」

先回到題目，題目給了我們一個檔案，我們打開它：

Decrypt my super sick RSA:
c: 964354128913912393938480857590969826308054462950561875638492039363373779803642185
n: 1584586296183412107468474423529992275940096154074798537916936609523894209759157543
e: 65537

總之就是請你用 RSA 解密，題目給你 c, n, e ，這裡的 n 當然是大寫 N ，不然你就直接有答案了。
所以我改一下變成這樣 (n 改 N)：

Decrypt my super sick RSA:
c: 964354128913912393938480857590969826308054462950561875638492039363373779803642185
N: 1584586296183412107468474423529992275940096154074798537916936609523894209759157543
e: 65537

我們從上面看到解密需要 c, d, N ，但是題目給 c, e, N ，缺 d 。
大家往上看到我寫的拿到密鑰的 4 點，你要 d 必須有 e, r ， e 有了，
我們缺的是 r ，而 r 從 (p-1) * (q-1) 來，所以需要 p, q 。

這就驗證了最重要的數字是 p, q 兩人，你唯一有的資訊是由他們倆乘起來的 N ，
意思就是你必須對 N 做質因數分解才能得到 p, q ，但你可以看看 N 到底多大...
基本上一般情況你用一般電腦是沒辦法對那麼大的數做質因數分解的，
數字太大幾萬年都做不到，這也是 RSA 相對安全的地方。

但是這題的 N 我們可以馬上解出來，歸功於 factordb 這個工具！
這個字直翻其實就是因數資料庫 (factor database) ，
它紀錄著許多已知的質因數分解，包括非常大的數在內。

這題沒有為難你，因為題目給的 N 是可以在 factordb 查到分解結果的，
factordb 連進網站，貼上 N：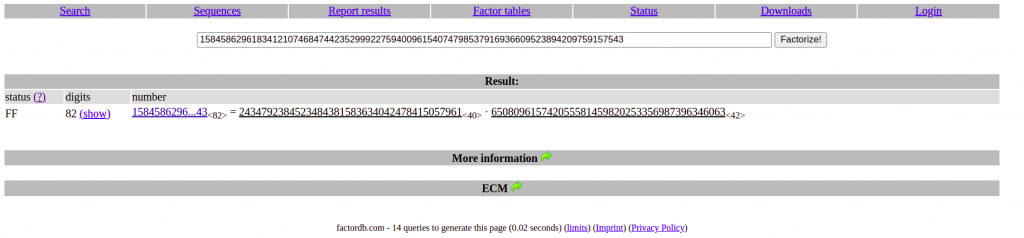

N 就等於
2434792384523484381583634042478415057961
x
650809615742055581459820253356987396346063
而這兩個數就是 p, q 。

要記得這件事絕沒那麼容易，這是題目給你剛好有分解資料的，否則幾乎不可能解出。

有了 p, q 其實答案就呼之欲出了，但我們需要動手寫程式：

c = 964354128913912393938480857590969826308054462950561875638492039363373779803642185
N = 1584586296183412107468474423529992275940096154074798537916936609523894209759157543
p = 2434792384523484381583634042478415057961  # factordb 找到的
q = 650809615742055581459820253356987396346063  # factordb 找到的
e = 65537
r = (p-1) * (q-1)
d = pow(e, -1, r)  # 求 e mod r 的乘法反元素 d
ans = pow(c, d, N)  # 求 c 的 d 次方 mod N 就是原本的明文

b = bin(ans)[2:]  # 明文轉成二進位表示
b = '0' + b  # 可以由二進制字串長度發現長度不是 8 的倍數，前面要補 0
i = 0  # 下面準備每八個切成一組表示成字元
for i in range(len(b)//8):
    j = i*8
    print(chr(int(b[j:j+8], base=2)), end='')
print()

其中 pow() 的用法呢，求乘法反元素的部份需要在 Python 3.8 以後才能使用，
而 pow(a, b, c) 的格式代表「 a 的 b 次方 mod c 」，如果是乘法反元素，
「求 e mod r 的乘法反元素 d」數學上會表示成「 d = e 的 -1 次方 mod r 」，
才會寫成 pow(e, -1, r) 。

最後 print 出 picoCTF{sma11_N_n0_g0od_73918962} 。 ( 你的 flag 跟我不一樣 )